Real-Time Polygonal-Light Shading with Linearly

读Real-Time Polygonal-Light Shading with Linearly Transformed Cosine

概述

这篇论文使用一个线性变换（Linearly Transformed Coines）将原本的BSDF分布转换到clamped consine上，利用这种近似方法可以求出一个区域光（Area Light）近似的解析解。

定义

要被变换的原始分布

原始的分布被记为$D_o$。它的选择控制了变换之后的分布的基本形状。

线性变换

为了生成一个新的分布$D$，可以将一个线性变换$M$应用到方向角$\omega_o$上。这个转换过程其实不一定是线性的：$\omega=M\omega_o/\|M\omega_o\|$，同时逆变换为$\omega_o=M^{-1}\omega/\|M^{-1}\omega\|$。

近似形状的表达式

在$\omega$处的LTSD的大小等于原始的分布$D_o$在$\omega_o$处的大小乘上立体角大小之比，公式(1):

$D(\omega)=D_o(\omega_o)\frac{\partial\omega_o}{\partial\omega}=D_o(\frac{M^{-1}\omega}{\|M^{-1}\omega\|})\frac{|M^{-1}|}{\|M^{-1}\omega\|^3}$

其中$\frac{\partial\omega_o}{\partial\omega}=\frac{|M^{-1}|}{\|M^{-1}\omega\|^3}$。

形状不变

在一种线性变换——缩放（$M=\lambda I$）下，因为缩放不影响方向角$\omega$的方向，所以不会改变分布。

特性

正规化

变换后分布$D$继承了原始分布的一些属性$D_o$。LSTD$D$的范数和原始分布$D_o$是一致的，因此通过公示(1)可以得到，公式(2): $\int_{\Omega}D(\omega)\mathrm{d}\omega=\int_{\Omega}D_o(\omega_o)\frac{\partial\omega_o}{\partial\omega}\mathrm{d}\omega=\int_{\Omega}D_o(\omega_o)\mathrm{d}\omega_o$

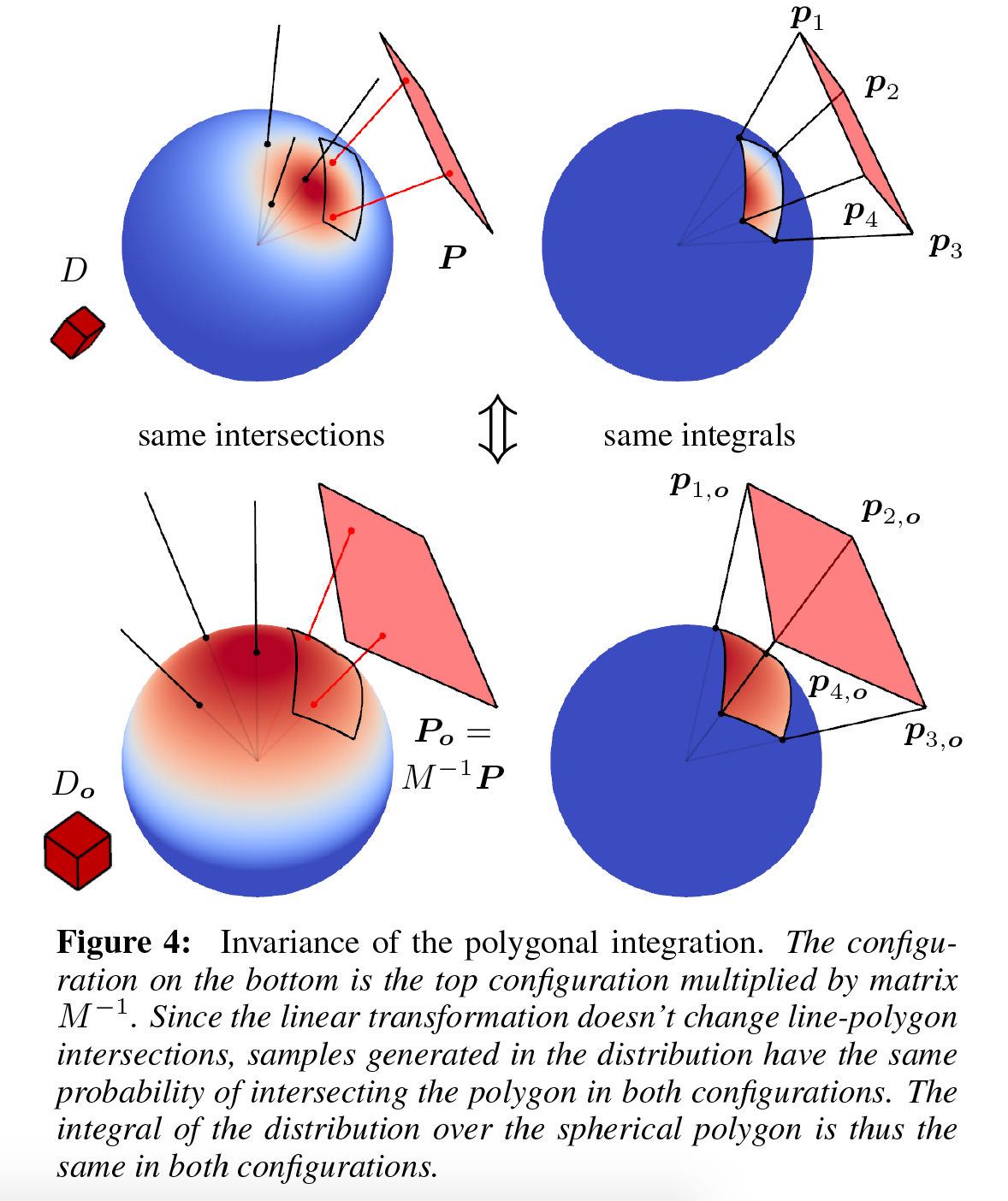
在多边形上的积分

在LTSD$D$分布在多边形$P$区域上的积分就等于原始分布$D_o$在多边形$P_o=M^{-1}P$上的积分。因此可以得到公式(3): $\int_{P}D(\omega)\mathrm{d}\omega=\int_{P_o}D_o(\omega_o)\mathrm{d}\omega_o$

用LTC近似基于物理的BRDFs

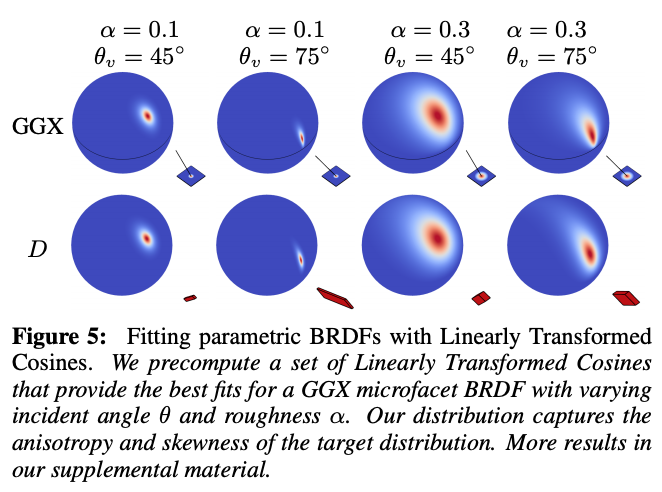
使用clamped cosine分布作为原始分布可以产生一族线性变换之后的分布，可以很好地近似BRDFs。

Linearly Tranformed Cosines

对于半球面上的clamped cosine分布可以这样表示，公式(4): $D_o(\omega_o=(x,y,z))=\frac{1}{\pi}\max(0,z)$

拟合（Fitting）

本文的近似目标是GGX 微表面 BRDF。精确地说目标拟合的公式是这样的： $D\approx \rho(\omega_v,\omega_l)\cos{\theta_l}$ 对一个各向同性的材料来说，BRDF取决于入射角度$\omega_v=(\sin{\theta_v},0,\cos{\theta_v})$和粗糙度$\alpha$。因此，对于任意一个$(\theta)v,\alpha)$组合，都要找出一个矩阵$M$能最好你和他，由于平面BRDF的各向同性，以及LTC的缩放不变性，M可以表示为，公式(6) $M=\begin{bmatrix} a & 0 & b \\ 0 & c & 0 \\ d & 0 & 1 \end{bmatrix}$ 因此，有四个参数需要拟合，作者的经验是最小化$L^3$误差能产生一个最好的结果。

存储

根据公式(3)可以看到，在任何情况下，其实都只需要一个逆矩阵$M^{-1}$，对各向同性的BRDF，矩阵可以由4个参数决定。另外，还需要一位记录拟合的BRDF的范数$\int_{\Omega}\rho(\omega_v,\omega_l)\cos{\theta_l}\mathrm{d}\omega_l$，所以一共需要5个参数。使用一个分辨率为$64 \times 64$的2D的纹理来记录，其中$\theta \in [0,\frac{\pi}{2}]$，$\sqrt{a} \in [0, 1]$

计算过程

计算收到的多边形光源的扩散(Diffuse)光，意味着计算在这个多边形域上光照度的积分，公式(7): $I=\int_{P}L(\omega_l)\rho(\omega_v,\omega_l)\cos{\theta_l}\mathrm{d}\omega_l$ 其中$\omega_v$是支教方向，$\rho$是BRDF，$P$是多边形，$L$是在$\omega_l$角上收到的多边形光源发出的辐射。为了使用LTC，在运行时，我们取出LTC$D$的$M^{-1}$、入射角$\theta_v$和BSDF的粗糙度$\alpha$，因此可以将公式(7)近似为公式(8): $I=\int_{P}L(\omega_l)\rho(\omega_v,\omega_l)\cos{\theta_l}\mathrm{d}\omega_l\approx\int_{P}L(\omega_l)D(\omega_l)\mathrm{d}\omega_l$ 接下来就可以用到之前所说的变换了变换了

着色辐射均匀的多边形光源

如果，多边形在空间上发出的辐射是一致的，那么$L(\omega_l)=L$，因此可以将辐射项提出积分公式，得到公式(9): $I=\int_{P}L(\omega_l)D(\omega_l)\mathrm{d}\omega_l=L\int_{P}D(\omega_l)\mathrm{d}\omega_l$ 由于之前所说的公式(3)，可以将分布$D$转换会原始分布$D_o$上去，从而得到公式(10): $\int_{P}D(\omega)\mathrm{d}\omega=\int_{P_o}D_o(\omega_o)\mathrm{d}\omega_o=E(P_o)$ 其中，$E$表示多边形$P_o=M^{-1}P$的辐射。而这个辐射可以用公式(11)近似计算: $E(p_1,...,p_n)=\frac{1}{2\pi}\sum_{i=1}^{n}\arccos(\langle p_i,p_j\rangle)\langle \frac{p_i\times p_j}{\|p_i\times p_j\|},\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\rangle$ 其中$j=(i+1)\mod n$。需要注意的是，这里需要提前将位于球面下侧的多边形裁减掉。

着色带纹理的多边形光源

本章介绍了如果光的颜色是用二维的彩色纹理表示的情况。此时公式(8)需要被重写为公式(12): $I\approx\int_{P}L(\omega_l)D(\omega_l)\mathrm{d}\omega_l=I_DI_L$ 其中 $I_D=\int_{P}D(\omega_l)\mathrm{d}\omega_l$ $I_L=\frac{\int_{P}L(\omega_l)D(\omega_l)\mathrm{d}\omega_l}{\int_{P}D(\omega)\mathrm{d}\omega_l}$ 这样做的好处是将公式分解了，因为这两部分有不同的性质。

高光的形状

$I_D$可以按照之前的公式进行计算，它描述在积分的大小，体现在高光部分的形状上。

高光的颜色

$I_L$可以被看作在某处的平均颜色，可以表示为一个纹理空间的滤波的结果，因此通过对颜色纹理的预先高斯滤波可以获得$I_L$的近似值。

纹理的预先滤波

根据$I_L$的定义，可以将它看作纹理$L$一个滤波器$F(\omega_l)=\frac{D(\omega_l)}{\int_{P}D(\omega_l)\mathrm{d}\omega_l}$，而这个公式可被近似为对纹理空间的一个高斯滤波。这个近似还需要满足两个条件：

1. 在球面之下的部分$F=0$，也就是说，光不能从平面下泄露出来。
2. 在纹理内$F$是正规化的，$\int_{P}F(\omega_l)\mathrm{d}\omega_l=1$

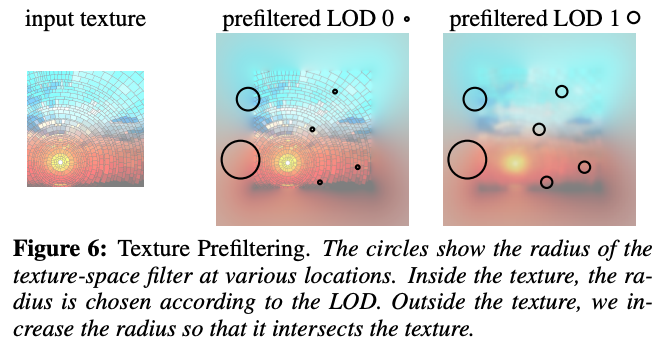
为了做到这个，需要在纹理中裁剪并重新正规化纹理空间高斯。需要在纹理的边缘增加一个边缘，在边缘上时扩大滤波的半径使他能和纹理相交。在边缘的外部，需要将坐标裁剪到边缘。结果类似下图：

如何取纹理

取纹理的部分需要有两个参数：纹理的坐标和LOD。直接计算平均向量和纹理的交点会有一定问题，因为有的时候纹理可能和平均向量根本没有交点。同时计算LOD也不方便。

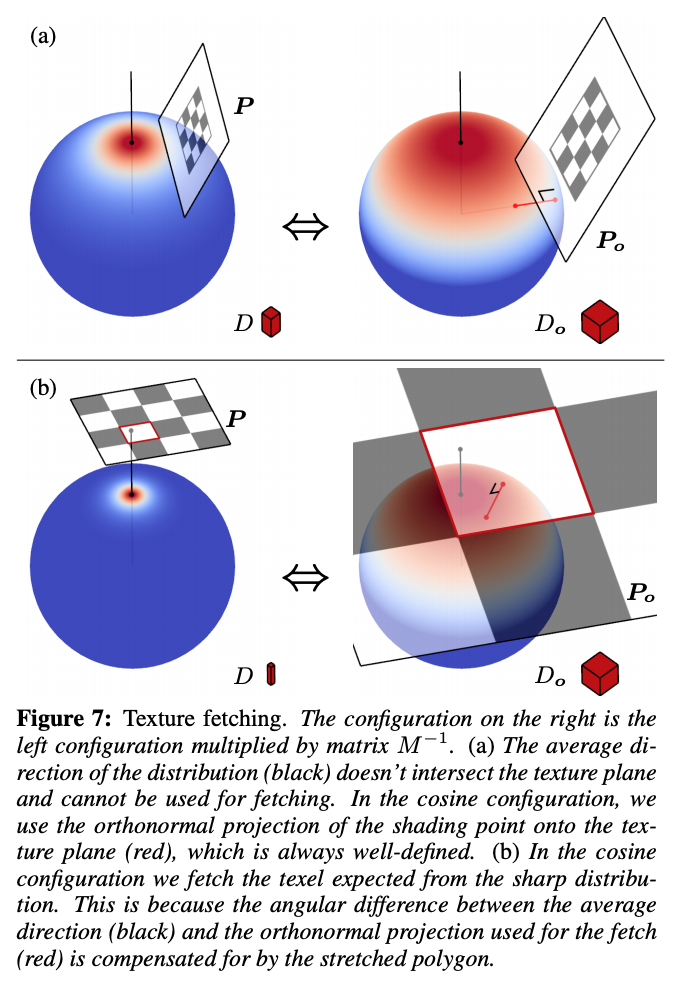
为了解决这个问题，依然是将分布转换回原始分布，利用公式(15): $I_L=\frac{\int_{P}L(\omega_l)D(\omega_l)\mathrm{d}\omega_l}{\int_{P}D(\omega_l)\mathrm{d}\omega_l}=\frac{\int_{P_o}L(\omega_l)D_o(\omega_l)\mathrm{d}\omega_l}{\int_{P_o}D_o(\omega_l)\mathrm{d}\omega_l}$ 根据作者的说法，这样做的好处是在$D_o$分布下参数化纹理空间的滤波更加简单、鲁棒。

取得预滤波的纹理

现在取纹理颜色只要取得着色点正交投影在纹理上的位置的颜色即可。因为用的是正交投影说一没有各向异性的问题，LOD的大小为到纹理平面的距离的平方$r^2$和多边形大小$A$的比值，鲁博士使用的高斯滤波的标准差为$\sigma=\sqrt{\frac{r^2}{2A}}$。

至此，本文的主要思想就介绍完了。